Strictly singular operator
In functional analysis, a branch of mathematics, a strictly singular operator is a bounded linear operator L from a Banach space X to another Banach space Y, such that it is not an isomorphism, and fails to be an isomorphism on any infinitely dimensional subspace of X. Any compact operator is strictly singular, but not vice-versa.[1][2]
Every bounded linear map 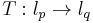 , for
, for 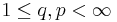 ,
, 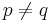 , is strictly singular. Here,
, is strictly singular. Here,  and
and 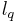 are sequence spaces. Similarly, every bounded linear map
are sequence spaces. Similarly, every bounded linear map 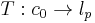 and
and 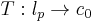 , for
, for 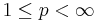 , is strictly singular. Here
, is strictly singular. Here 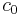 is the Banach space of sequences converging to zero. This is a corollary of Pitt's theorem, which states that such T, for q < p, are compact.
is the Banach space of sequences converging to zero. This is a corollary of Pitt's theorem, which states that such T, for q < p, are compact.